Introduction

Aujourd’hui la plupart des entreprises et plus précisément les entreprises spécialisées dans l’informatique décisionnelle, font des séries temporelles afin d’étudier les variables au cours du temps.

L’étude des séries temporelles a pour objectif de déterminer le trend et la saisonnalité au cours du temps et de savoir si le processus est linéaire ainsi d’estimer les modèles ARMA et ARIMA et faire des previsions à la fin.

ces séries ont une structure fondée sur les bases de données, fournissant ainsi le volume nécessaire d’information permettant de dresser une série chronique historique des événements passés dans le but de prévoir le futur.

Après avoir défini les séries temporelles, notre projet va consister à étudier, modéliser et prédire deux séries temporelles différentes sur une même période.

Données : Ventes de gazole (en kt)

La série chronologique étudiée représente les ventes mensuelles de gazole (en Kt) du 01 janvier 1981 au 01 novembre 2016.

autoplot(gazolets, main="Ventes de gazole en kt")

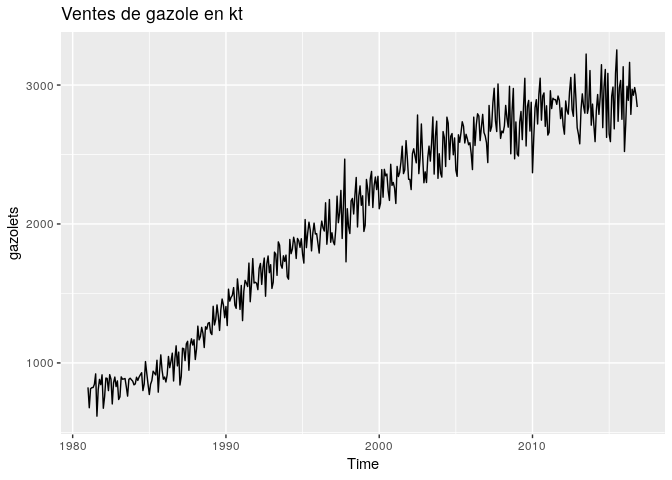
La figure ci-dessus représente la série. Les premières observations que nous pouvons faire à partir de cette série sont les suivantes : - La série a une tendance croissante. - La série a une périodicité, du fait de sa succession de croissance et de décroissante au fil du temps. - La série est multiplicative, du fait que l’amplitude de sa période augmente avec le temps. - On peut utiliser le log de la série pour supprimer cette variation d’amplitude dans la série. - La série n’est pas stationnaire, la variance n’est pas constante dans le temps.

Caractéristiques de la série.

Certaines remarques ont été faite à la première observation de la série, cependant il conviendrait de vérifier ces appréhensions et de poser certaines hypothèses si nécéssaires de sorte à pouvoir cerner toutes les caractéristiques de la série.

Nous passons au log des données afin de pouvoir réduire les variations d’amplitude dans le temps.

autoplot(log(gazolets), main="log des Ventes de gazole en kt")

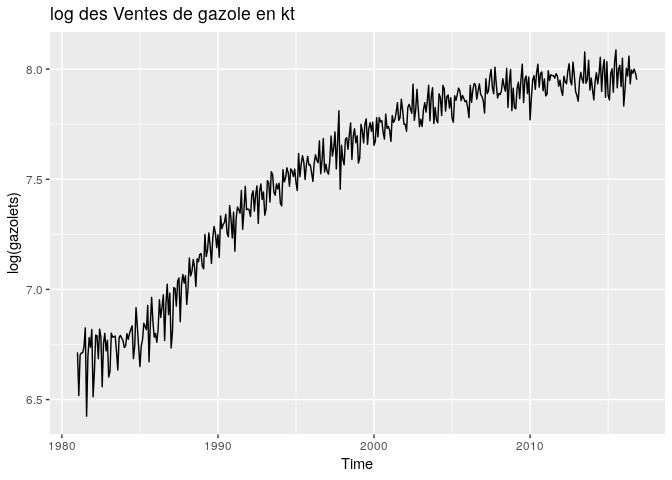
En observant le log de la série, la variation d’amplitude n’ont pas totalement disparu, de plus la tendance présente désormais une certaine courbure. En passant au log, le problème d’amplitude n’a pas été résolu de façon satisfaisante, pour la tendance, plus elle est linéaire, mieux nous pouvons l’observer de façon globale.

Test de stationnarité de la série.

Augmented Dickey-Fuller Test

Le tes de Dickey-Fuller, effectue un test de stationnarité de la série avec pour hypothèse nulle, la série n’est pas stationnaire avec un seuil d’erreur de 5%.

adf.test(gazolets)

##
##  Augmented Dickey-Fuller Test
##
## data:  gazolets
## Dickey-Fuller = -2.0903, Lag order = 7, p-value = 0.5394
## alternative hypothesis: stationary

On ne rejette pas l’hypothèse nulle la p-value étant supérieur au seuil de 5%, la série est donc non stationnaire.

Hypothèse de stationnarité par l’autocorrélogramme (ACF)

Cette hypothèse peut être confirmée ou infirmée par l’observation de l’autocorrelogramme de la série. En effet une série stationnaire à un autocorrélogramme qui décroit de façon exponentielle vers 0.

ggAcf(gazolets, main="Vente de gazole en kt")

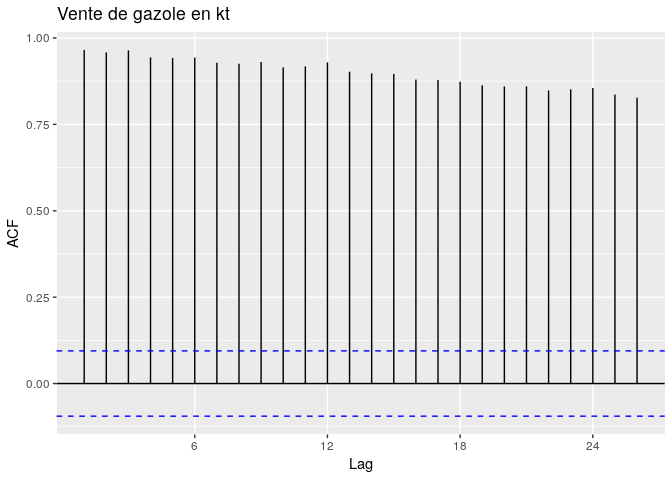
L’autocorrellogramme ne décroît pas de façon exponentielle vers 0, par contre on observe des grands piques aux lags 1, 12, 24. ce qui pourrait représenter la périodicité de la série. La période la série peut-être confirmée par la fonction frequency de R.

frequency(gazolets)

## [1] 12

Décomposition de la série :

Nous avons observé à première vue que la série est multiplicative, du fait de l’augmentation de l’amplitude de sa périodicité dans le temps, et de la forme horizontale de tendance à partir d’un certain temps.Observons sa décomposition multiplicative et comparons la avec sa décomposition additive dans la figure ce dissous.

par(mfrow=c(1,2))
autoplot(decompose(gazolets, type = "multiplicative"))


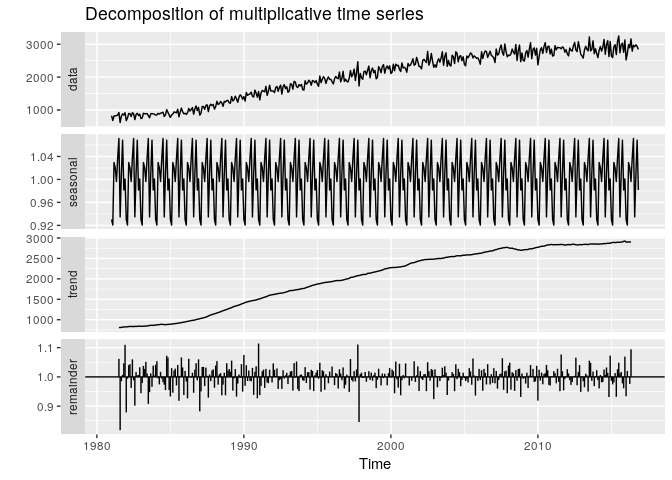
autoplot(decompose(gazolets, type = "additive"))

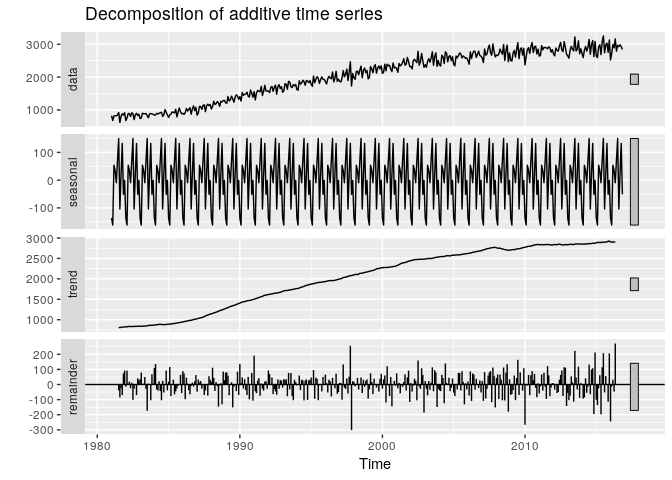
La décomposition en multiplicative et additive ne varie que sur les résidus, le trend et la saisonnalité restent plus ou moins identiques pour les deux méthodes de décomposition. Dans la suite nous pouvons donc supposer que la série est additive.

Conlusion

En résumé, les caractéristiques de la série sont les suivantes :

  • Non stationnaire
  • additive
  • tendance croissante
  • périodique de période 12

Modélisation puis calibration, de la série ventes de gazole

La section précédente nous a permis de conclure sur une série non-stationnaire, saisonnière de saisonnalité 12. La modélisation consiste à trouver le modèle de série chronologique qui saura reproduire au mieux la série. Le choix logique de ce modèle pour l’estimation de la série est un modèle Seasonnal ARIMA (p,d,q)(P,D,Q) (SARIMA). Les coefficients de ce modèles sont eux aussi fournis par les caractéristiques de la série. Le choix de ces coefficients représentent la principale difficulté, cependant nous pouvons observer différentes transformations de la série afin d’orienter nos différents choix. Tout d’abord explicitons les différentes significations de ces coefficients :

  • p : AR de la partie non saisonnière de la série
  • d : Degré d’intégration de la partie non saisonnière de la série
  • q : MA de la partie non saisonnière de la série
  • P : AR de la partie saisonnière de la série
  • D : Degré d’intégration de la partie saisonnière de la série
  • Q : MA de la partie saisonnière de la série

Le bon modèle, sera celui dont les coefficients permettent d’obtenir un bruit banc comme résidus. Les résidus doivent suivre une loi normale de moyenne nulle, de variance constante et sans autocorrélation. L’objectif de la modéliser la série est de pouvoir prédire un certain nombre de valeurs futures avec un minimum de marge d’érreur.

Stationnarisation de la série

La première étape essentielle est la stationnarisation de la série. IL existe plusieurs manières de le faire, mais le plus important est de choisir une série stationnaire qui permettrait de choisir les bons coefficients. Nous choisissons une stationnarisation par différenciation de degré 2 au lag 12, pour supprimer la tendance et la saisonnalité.

d2X = dX**t* − *dXt − 12  avec*  *dX = Xt − Xt − 12

tsdisplay(diff(diff(gazolets,12),12), main = "la série vente de gazole différentiée")

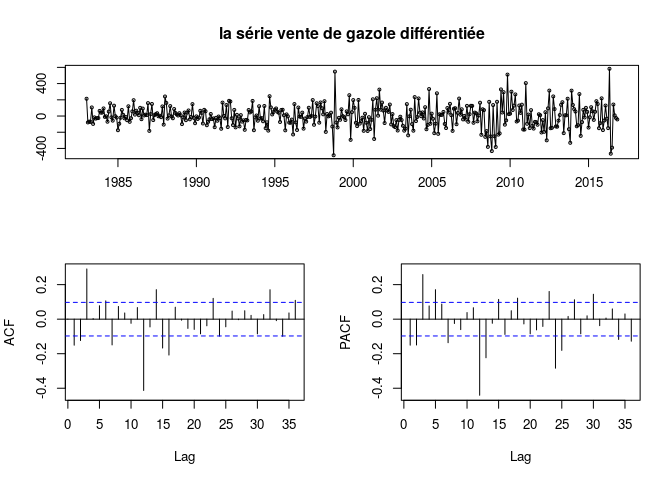
L’autocorrelograme de la série décroît de façon exponnentielle, avec un pique au lag 12 qui représente la saisonnalité aussi observé dans l’autocorrelogramme partiel.

adf.test(diff(diff(gazolets,12),12))

## Warning in adf.test(diff(diff(gazolets, 12), 12)): p-value smaller than
## printed p-value

##
##  Augmented Dickey-Fuller Test
##
## data:  diff(diff(gazolets, 12), 12)
## Dickey-Fuller = -6.0499, Lag order = 7, p-value = 0.01
## alternative hypothesis: stationary

Avec la confirmation du test de Dickey-Fuller augmenté (p-value inférieure à 5%) on obtient une série stationnaire.

Choix des paramètres p,d,q et P,D,Q

Le choix des paramètres (p,d,q)(P,D,Q), se font essentiellement sur la base de l’autocorrelogramme et de l’autocorrelogramme partiel.

Choix des paramètres p,d,q

Pour choisir les paramètres p,d,q qui représentent la modélisation de la partie non saisonnière, on observe l’ACF (autocorrélogramme) et le PACF (autocorrélogramme partiel) à partir du lag 1. L’appréciation de l’ACF permet le choix de q. On choisit q de sorte à pouvoir tenir compte des autocorrélations successives qui sortent de la zone d’acceptation (les lignes discontinuent bleues sur la figure). Par observation de l’ACF (ci-dessous), les trois premières autocorrélations sont très significatives, surtout la troisième, donc un candidat est q = 3 .

ggAcf(diff(diff(gazolets,12),12), main = "Autocorrélogramme de la série vente de gazole différentiée")

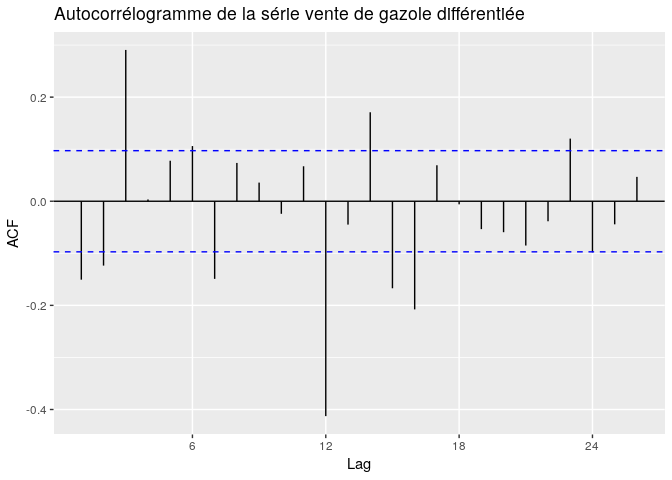
Quant à p, il est choisi sur le même principe que le q mais appliqué au PACF. On observe les premières autocorrélations partielles, c’est à dire à partir de 1, et on prend le coefficient qui tient compte des piques qui sont hors de la zone d’acceptation (autocorrélation partielle est nulle pour le lag correspondant) . Des candidats possibles à p sont p = 3 , p = 5 .

ggPacf(diff(diff(gazolets,12),12),main="Autocorrélogramme partiel de la série vente de gazole différentiée")

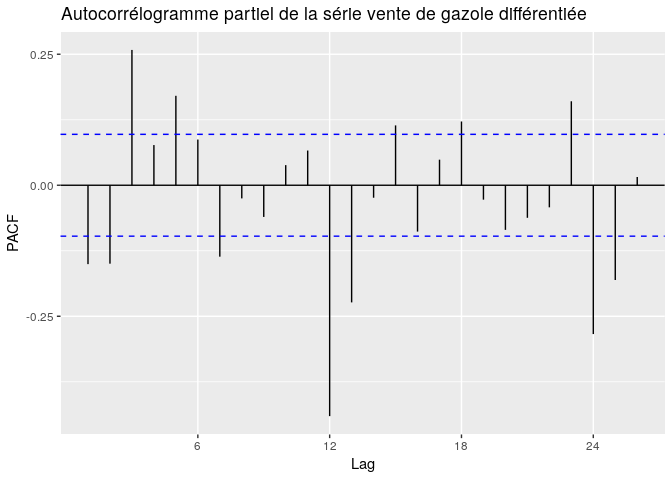
Le paramètre d représente le degré de différenciation de la partie non saisonnière, vu que la série n’a été différentiée deux fois au lag 12, c’est à dire que sur la période, on suppose que la partie non saisonnière n’a pas été différenciée

Choix des paramètres P,D,Q

Les paramètres P,Q se choisissent sur les mêmes critères que p,d,q mais appliqués à la partie saisonnière. Pour le choix de ces paramètres, on observe l’ACF et le PACF mais à partir du lag de la période, c’est à dire 12. Donc les paramètres seront choisis afin de tenir compte des piques significatifs à partir du lag 12, contrairement à la partie non saisonnière qui commence au lag 1. Donc d = 0 . Le paramètre D représente le degré de différenciation de la partie saisonnière c’est à dire D = 2.

Conclusion

Les modèles candidats sont donc SARIMA*(3, 0, 3)(2, 2, 3)12 et *SARIMA(5, 0, 3)(2, 2, 3)12 .

Calibration des modèles à la série

La calibration consiste à estimer les coefficients du modèle choisi à partir de la série.

SARIMA(3,0,3)(2,2,3)

Le premier modèle appliqué est le modèle : SARIM**A(3, 0, 3)(2, 2, 3)12 .

Les résultats de calibration sont :

##
## Call:
## arima(x = gazolets, order = c(3, 0, 3), seasonal = list(order = c(2, 2, 5)),
##     method = "ML")
##
## Coefficients:
##           ar1     ar2     ar3     ma1     ma2      ma3     sar1     sar2
##       -0.1608  0.1653  0.9928  0.2461  0.0545  -0.8065  -1.2133  -0.9434
## s.e.   0.0053  0.0051  0.0049  0.0274  0.0289   0.0263   0.0356   0.0349
##          sma1     sma2     sma3    sma4    sma5
##       -0.4012  -0.5882  -0.7805  0.5173  0.3665
## s.e.   0.0903   0.0806   0.0893  0.0928  0.0686
##
## sigma^2 estimated as 4077:  log likelihood = -2318.17,  aic = 4664.34

tsdiag(out, gof.lag=60)

L’exécution de ce modèle sous R renvoie le message, “problème de convergence possible : optim renvoie un code = 1”, et fourni des résultats assez mauvais. Donc il est exclu de nos modèles.

SARIMA(5,0,3)(2,2,3)

Le deuxième modèle appliqué est le modèle : SARIM**A(5, 0, 3)(2, 2, 3)12 .

Les résultats de calibration sont :

##
## Call:
## arima(x = gazolets, order = c(5, 0, 3), seasonal = list(order = c(2, 2, 5)),
##     method = "ML")
##
## Coefficients:
##           ar1      ar2     ar3     ar4    ar5     ma1     ma2      ma3
##       -0.5481  -0.0845  1.0283  0.4179  0.185  0.4263  0.2222  -0.6593
## s.e.   0.0754   0.0792  0.0190  0.0791  0.076  0.0598  0.0699   0.0516
##          sar1     sar2     sma1     sma2     sma3   sma4    sma5
##       -1.2234  -0.9582  -0.4846  -0.6092  -0.7866  0.631  0.3550
## s.e.   0.0315   0.0301      NaN      NaN   0.0918    NaN  0.0149
##
## sigma^2 estimated as 3567:  log likelihood = -2303.27,  aic = 4638.55

Test d’autocorrélation de Ljung-Box sur les résidus

Le test d’autocorrélation de Ljung-Box sur les résidus fourni les résultats suivants:

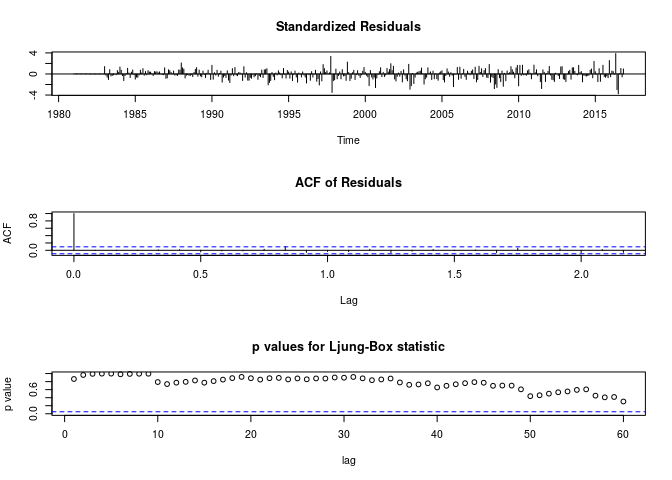
La figure ci-dessus représente les residus, l’ACF des résidus et le test Ljung-Box static, qui fourni l’hypothèse de non autocorrélation des résidus jusqu’au lag 60.

Test de normalité des résidus

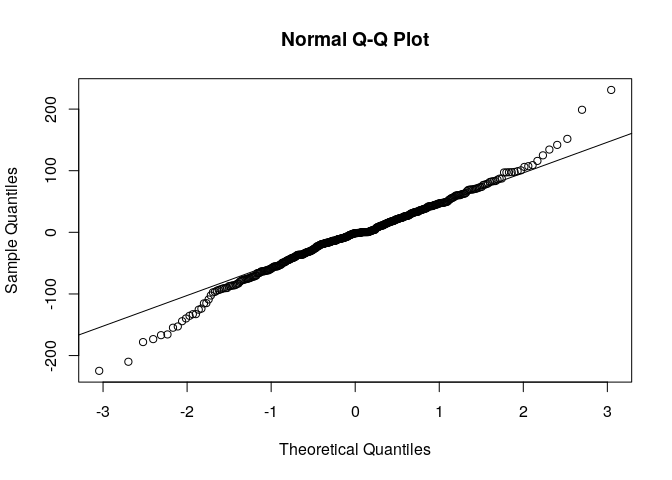
Avec le test de normalité ci dessus, nous pouvons supposer que les résidus suivent une loi normale, doc qu’on a bien un bruit blanc. Mais nous restons conscient que cette hypothèse est très limite et qu’il y’aurait moyen de fair mieux en choisisant un meilleur modèle. Cependant il faudrait éviter les modèles avec un très grand nombre de paramètre à estimer sysnonyme d’erreurs d’estimation.

Prédiction sur 1 an de Vente de Gazole

A partir du modèle estimé, nous pouvons faire une prédiction sur les 12 mois suivant de la série.

predict(out, n.ahead = 12)

## $pred
##           Jan      Feb      Mar      Apr      May      Jun      Jul
## 2016                                                               
## 2017 2594.158 2734.008 2856.113 2869.177 2983.947 2856.900 3098.031
##           Aug      Sep      Oct      Nov      Dec
## 2016                                     2906.565
## 2017 2859.767 2874.374 3059.186 2818.495         
##
## $se
##           Jan      Feb      Mar      Apr      May      Jun      Jul
## 2016                                                               
## 2017 62.04433 63.30826 65.41229 65.89004 67.67989 68.67473 69.35119
##           Aug      Sep      Oct      Nov      Dec
## 2016                                     61.63214
## 2017 71.16689 71.91184 72.69809 74.41613

pred : la prédiction, se : l’erreur d’estimation.

autoplot(forecast(out,h=12))

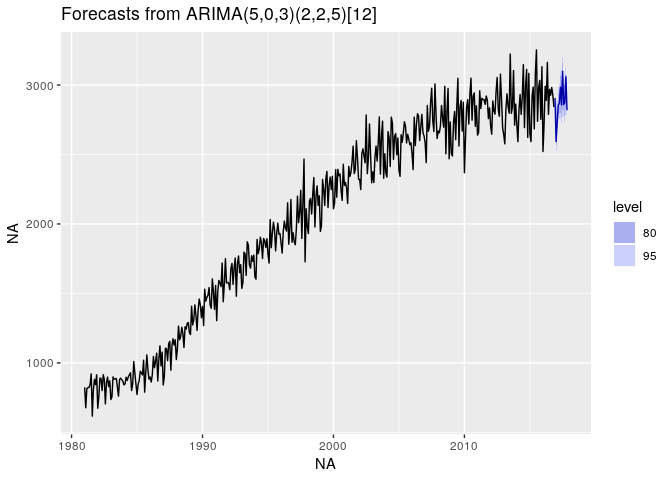
Le graphique ci dessus représente la série de vente de gazole (en kt) ainsi que la prédiction sur les 12 mois suivants.

Données : Ventes de super carburant (en kt)

La série chronologique étudiée représente les Ventes mensuelles de super carburant (en Kt) du 01 janvier 1981 au 01 novembre 2016. L’étude de cette série a les même étapes que la série précédente, nous allons observer puis en tirer des conclusions sur les caractéristiques de la série.

La série se présente comme suit :

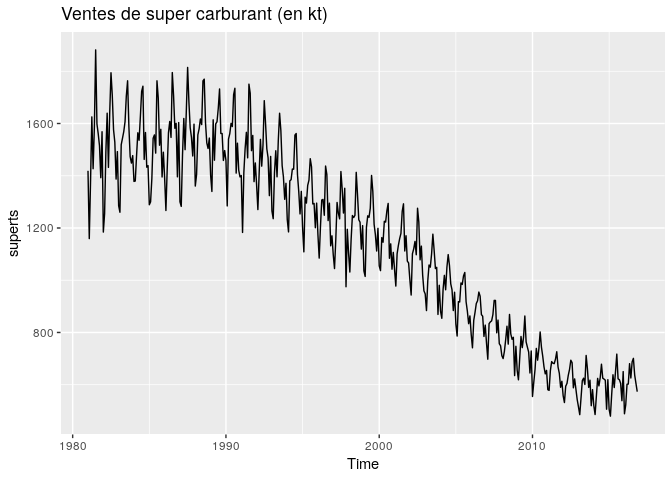
Caractéristiques de la série supercarburant

En premier lieu nous avon besoin de savoir si la série est stationnaire ou non. Par observation nous voyons bien qu’elle ne l’est pas et nous pouvons le confirmer par le tes de Dickey-Fuller augmenté.

adf.test(superts)

##
##  Augmented Dickey-Fuller Test
##
## data:  superts
## Dickey-Fuller = -3.4328, Lag order = 7, p-value = 0.04904
## alternative hypothesis: stationary

La p-value est sensiblement de 5%, la série n’est donc pas stationnaire par hypothèse.

Nous pouvons aussi observer l’autocorrelogramme (ACF) de la série.

ggAcf(superts, main="autocorrelogramme Ventes de super carburant (en kt)")

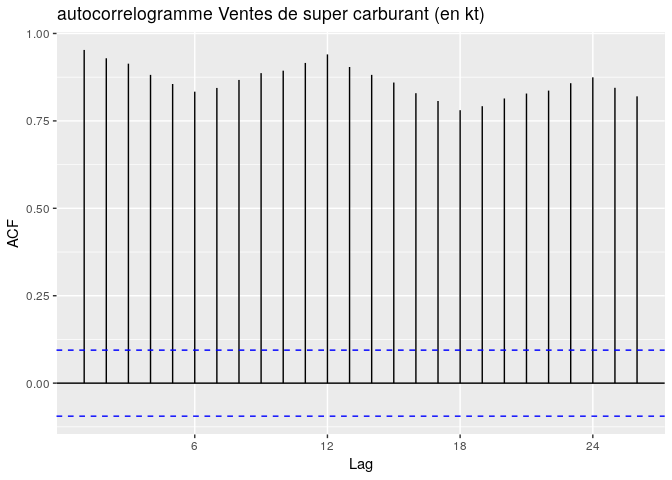
l’ACF décroit très lentemment vers 0 avec des piques périodiques de période 12. La série n’est donc pas stationnaire, mais elle a une saisonnalité de 12.

Nous supposons que la série est additive, ce qui nous donne la décomposition suivante :

autoplot(decompose(superts, type = "additive"))

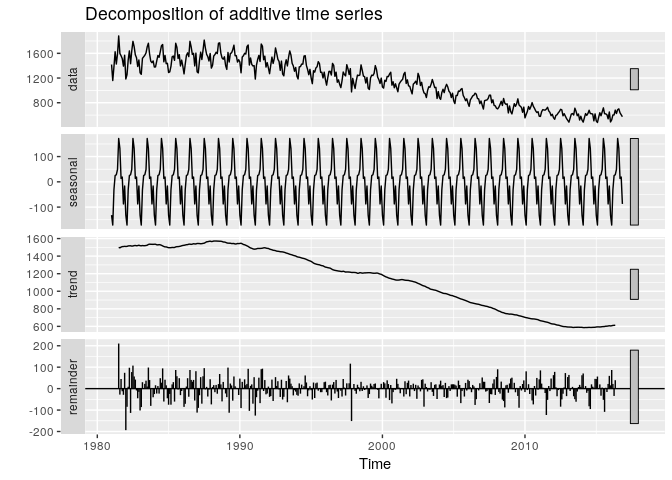
On observe une tendance décroisante et la saisonnalité.

En résumé, les caractéristiques de la série sont les suivantes :

  • Non stationnaire
  • additive
  • tendance décroissante
  • périodique de période 12

Modélisation de la série de vente de super carburant.

Comme pour la série de vente de gazole, un certain nombre de transformation dans un objectif de trouver le modèle de la série s’impose.

Stationnarisation de la série de vente de super carburant.

Commençons pas stationnariser la série. Nous la stationnarisons par la méthode des différentions sur la partie non saisonnière, c’est à dire de lag 1. Ainsi nous conservons la saisonnalité de la série.

autoplot(diff(superts), main="La série vente de Super carburant différentiée")

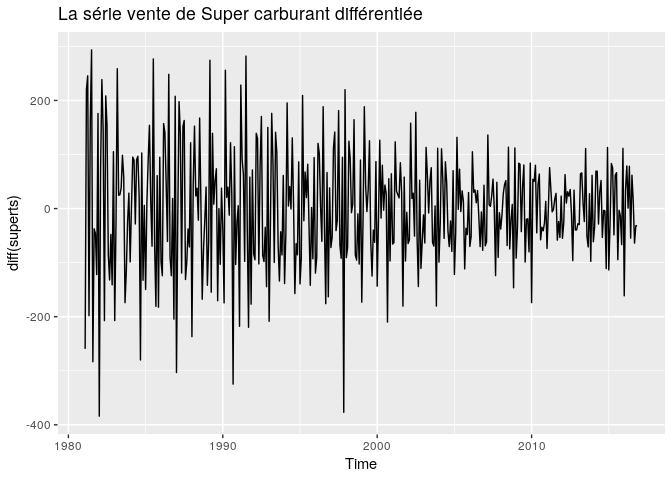
le test de Dickey-Fuller augmenté confirme bien une série stationnaire, vaec une pvalue inférieur à 5%.

adf.test(diff(superts))

## Warning in adf.test(diff(superts)): p-value smaller than printed p-value

##
##  Augmented Dickey-Fuller Test
##
## data:  diff(superts)
## Dickey-Fuller = -33.311, Lag order = 7, p-value = 0.01
## alternative hypothesis: stationary

Choix des paramètres p,d,q et P,D,Q

Comme pour la série de ventes de gazole, la série “vente de super carburant”, est non stationnaire et saisonnière, nous pouvons donc la modéliser par un modèle SARIMA.

L’estimation des paramètre sera fondé sur l’observation des autocorrélogramme et autocorrélogramme partiel.

ggAcf(diff(superts), main="Autocorrélogramme de la série vente de Super carburant différentiée")


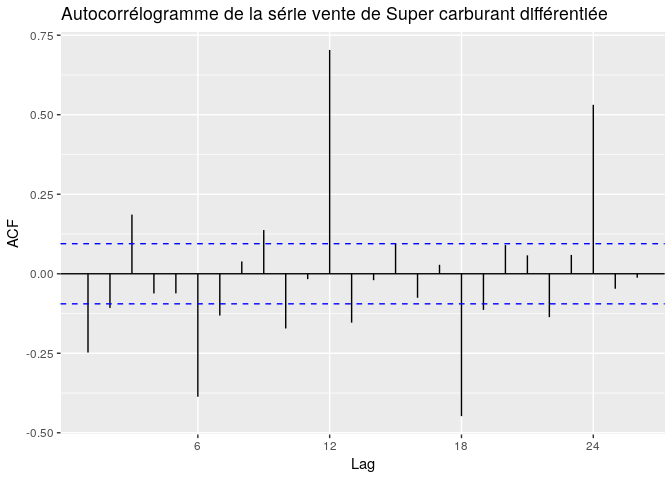
ggPacf(diff(superts), main="Autocorrélogramme partiel de la série vente de Super carburant différentiée")

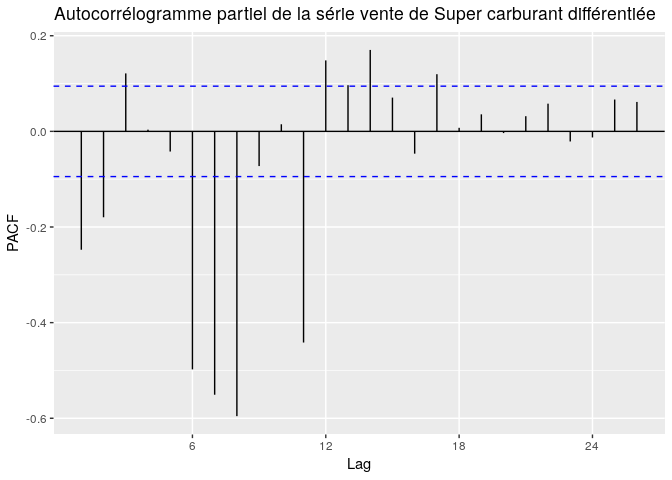
Choix des paramètres p,d,q

Le choix de ces paramètres sera la résultante des autocorrélations et des autocorrélations partielles à partir de la partie non saisonnière c’est àà dire à partir du lag 1. p, représentera le nombre d’autoccorélations partielles significatifs à modéliser, q, le nombre d’autoccrélation significatif et d le degré de différentiation.

Choix des paramètres P,D,Q

Le choix de ces paramètres sera la résultante de l’observation de la partie saisonnière de l’ACF et du PACF. avec D le degré de différentiation de la partie saisonnière.

Calibration des modèles à la série

Le meilleur modèle que nous ayons trouvé est le modèle SARIMA(3,1,2)(5,0,2).

Les résultats de calibration sont :

##
## Call:
## arima(x = superts, order = c(3, 1, 2), seasonal = list(order = c(3, 0, 2)),
##     method = "ML")
##
## Coefficients:
##           ar1     ar2     ar3      ma1     ma2    sar1    sar2    sar3
##       -0.1582  0.0714  0.3394  -0.9180  0.0509  0.6492  0.2175  0.1265
## s.e.   0.1744  0.0895  0.0658   0.1776  0.1310  0.2523  0.3039  0.0832
##          sma1     sma2
##       -0.2351  -0.3237
## s.e.   0.2500   0.1903
##
## sigma^2 estimated as 1716:  log likelihood = -2230.2,  aic = 4482.4

Test d’autocorrélation de Ljung-Box sur les résidus

Le test d’autocorrélation de Ljung-Box sur les résidus fourni les résultats suivants:

tsdiag(out2, gof.lag=60)

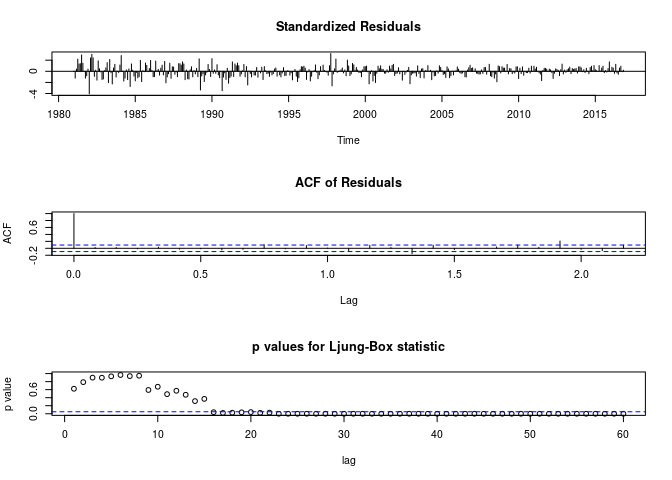
On observe une indépendance des résidus jusqu’au lag 60, on peut en conclure que les résidus sont non autocorrelés.

Test de normalité des résidus

Le test de normalité des résidus fourni les résultats suivants :

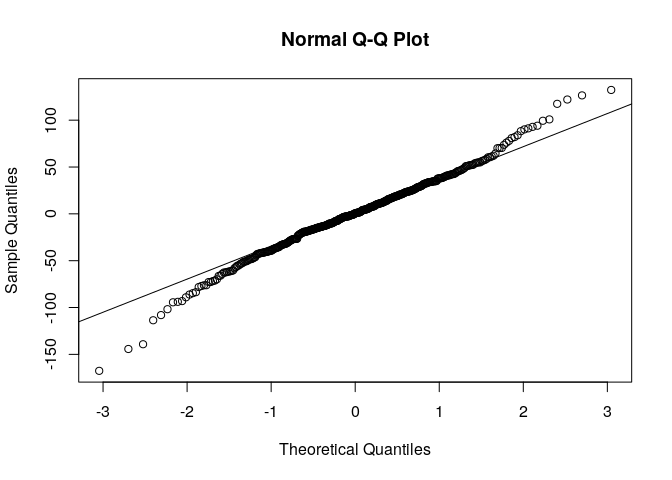
On peut considérer l’hypothèse que les résidus sont de loi normale. Mais en éliminant les valeurs extrèmes des résidus on peut arriver à une loi normale avec plus de certitude.

Prédiction sur 1 an de Vente de super carburant

Les valeurs de prédiction sur 1 an sont :

predict(out2, n.ahead = 12)

## $pred
##           Jan      Feb      Mar      Apr      May      Jun      Jul
## 2016                                                               
## 2017 509.6886 522.6831 584.5243 616.6773 647.5144 631.3322 690.6549
##           Aug      Sep      Oct      Nov      Dec
## 2016                                     618.2147
## 2017 674.5362 623.3480 612.1816 549.8391         
##
## $se
##           Jan      Feb      Mar      Apr      May      Jun      Jul
## 2016                                                               
## 2017 41.54220 42.49772 46.12154 46.17586 47.13719 48.23845 48.53091
##           Aug      Sep      Oct      Nov      Dec
## 2016                                     41.42216
## 2017 49.28865 49.93383 50.37594 50.99854

pred : la prédiction, se : l’erreur d’estimation.

autoplot(forecast(out2,h=12))

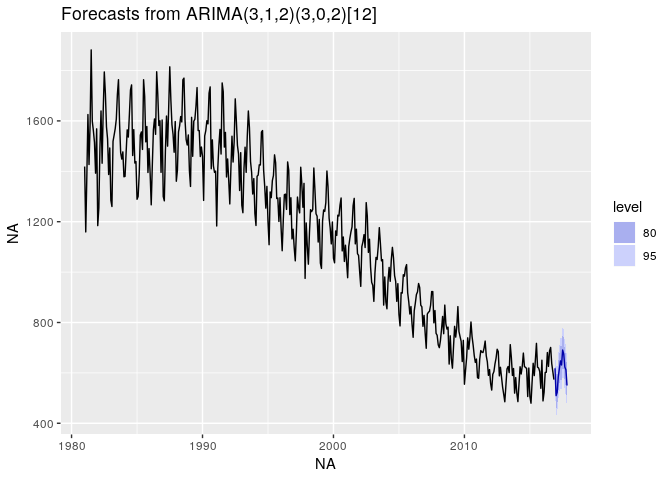
De façon générale on peut conclure que la prédiction ne trahi pas la structure de la série.

Conclusion

Dans notre projet, nous avons étudié deux séries. Cette étude avait pour but de modéliser, calibrer et prédire les séries. la modélisation a consisté à trouver des modèles qui vont les estimer avec le moins d’erreur possible. Pour les deux séries, le modèle SARIMA a été utilisé, du fait de la saisonnalité très présente des deux séries. Quant aux coefficients d’autorégression et de moyenne mobile, ils ont été choisis de façon sélective à partir de l’observation et de l’appréciation des autocorrélogramme et autocorrélogramme partiel. Nous avons testé un certain nombre de modèle, puis retenu ceux qui fournissaient des résidus sans autocorrélation (test de ljung-box) et de loi normale (test de normalité). Ensuite nous avons calibré les modèles choisis par la méthode de vraisemblance, c’est à dire que nous avons estimé les paramètres du modèle SARIMA. Après modélisation et calibration nous avons prédit les 12 prochaines valeurs des séries. Dans l’ensemble la prédiction ne trahi pas les structure des séries. Cependant nous somme conscient que les nodèles ne sont pas uniques, et qu’il est possible d’en trouver d’autres avec des meilleures performances d’estimation. Ces modèles peuvent êtres trouver en différenciant de différente façon les séries. Pour les deux séries, nous avions bien des résidus sans autocorrélation, mais pas forcément de loi normale et de moyenne nulle, à cause notemment des valeurs assez extrèmes présentes dans les résidus. Donc nous avons supposé que les résidus sont des bruits blancs et nous avons effectué les prédictions. Toute la difficulté des séries temporelles se trouvent dans la modélisation, et avec une étude plus approfondi et avec des moyens techniques et théoriques avancé, il est possible de “trouver” le meilleur modèle pour chacune des séries.