Prediction with decision trees (M)
- Importation des données
- Arbres de décision et Prédiction des données initiales
- Construction des intervalles pour chaque variable
- Transformation du tableau de données initial en tableau disjontif complet pour l’ACM.
- ACM
- Arbres de décision et Prédiction des données issues de l’ACM sur les données initiales
- Données renéttoyées : ACM, arbre de décision, CAH, kmeans
Importation des données
On importe tout d’abord les données, il le faut bien, c’est dessus qu’on travail! On a une base de données d’hopitaux anonimées, qui donne seulement leur type et leur quantité de prestation dans 23 domaines. l’objectif est de trouver une classification des données qui correspondra au 9 types d’établissement, et de retrouver le type d’un établissement à partir des autres variables. Prédiction du type d’établissement à partir des quantité de prestations.
(data version 0)
# Data mining projet
# M2 semestre 2
#sthda.com/mca
library(plotly)
## Loading required package: ggplot2
##
## Attaching package: 'plotly'
## The following object is masked from 'package:ggplot2':
##
## last_plot
## The following object is masked from 'package:stats':
##
## filter
## The following object is masked from 'package:graphics':
##
## layout
library(classInt)
#library(ade4)
############################################
# Import des données
############################################
df = read.csv("Hopitaux.csv")
# Nombre de type d'établissement
nbe = length(unique(df[,1]))
boxplot(df[,2:ncol(df)], use.cols = T)
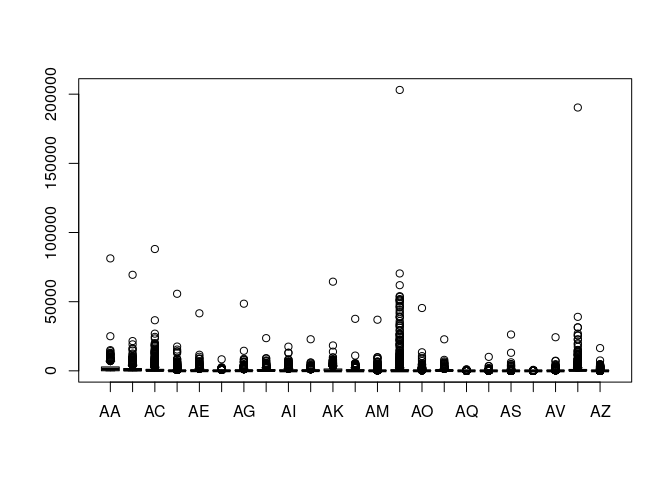
# Which max trouve l'index de la valeur maximale de la colonne en paramètre,
# valeur potentiellement abbérante
# La commande which.max permet de trouver la valeur maximale, la plus éloignée vers le haut dans
# le boxplot
# Supression de valeurs abérantes
# Supression de la 504
df5 = df[-which.max(x = df[, "AB"]),][-which.max(x = df[, "AN"]),][-which.max(x = df[, "AN"]),][-which.max(x = df[, "AC"]),][-which.max(x = df[, "AS"]),][-which.max(x = df[, "AI"]),][-which.max(x = df[, "AI"]),]
df5typeeta = df5[, 1]
df5 = df5[,-1]
Arbres de décision et Prédiction des données initiales
Arbre de décision des données initiales
on construit ici un arbre de décision sur les données, question d’évaluer les performances d’un arbre de décision.
# Prediction sur les données brut init
library(rpart)
library(party)
## Loading required package: grid
## Loading required package: mvtnorm
## Loading required package: modeltools
## Loading required package: stats4
## Loading required package: strucchange
## Loading required package: zoo
##
## Attaching package: 'zoo'
## The following objects are masked from 'package:base':
##
## as.Date, as.Date.numeric
## Loading required package: sandwich
## Create a formula for a model with a large number of variables:
# formule : prediction du type d'établissement en fonction des autres variables quantitaves
# application du dataframe initiale
fmla <- as.formula(paste("Type.Etablissement ~ ", paste(colnames(df5), collapse = "+")))
# creation de l'arbre à partir, formule, et données
type_eta = ctree(fmla, data = df)
# print(type_eta)
# plot de l'arbre de décision
#plot(type_eta, type = "simple")
Prédiction sur les données initiales
Tableau de confusion pour avoir une idée des performances de l’arbre et de la prédiction qu’elle engendre.
# prédiction à partir de l'arbre de prédiction
table(predict(type_eta), df$Type.Etablissement)
##
## CH1 CH2 CH3 CH4 CHU CLC HL pr PSP
## CH1 126 6 0 0 0 0 9 17 25
## CH2 9 58 12 0 0 0 0 5 8
## CH3 0 4 34 3 0 0 0 0 2
## CH4 0 0 12 155 4 0 0 1 3
## CHU 0 0 0 1 27 0 0 0 0
## CLC 0 0 0 1 0 19 0 0 0
## HL 16 0 0 0 0 0 139 4 9
## pr 11 8 9 3 0 0 13 686 50
## PSP 8 1 2 0 0 1 5 8 25
Taux de succès de prédiction
Calcul du taux de succès de la prédiction
(sum(predict(type_eta)==df$Type.Etablissement)) / nrow(df)
## [1] 0.8245614
Suppression de valeurs jugées abérantes de la prédiction
Après avoir construit un arbre à partir des donnée initiales comme données d’apprentissage, on remarque un taux de d’échec de prédiction. Supposons que les individus que l’arbre n’a pas prédit avec succès sont des individus abérants. Il suffit donc de les éliminer, et d’obtenir une base de données plus ou moins propre. A partir de cette nouvelle base, on reconstruit un arbre et on évalue le taux de succès de prédiction afin de la comparer au premier
(data version 1)
df_propre = df[df[,1]==predict(type_eta),]
## Create a formula for a model with a large number of variables:
# formule : prediction du type d'établissement en fonction des autres variables quantitaves
# application du dataframe initiale
fmla <- as.formula(paste("Type.Etablissement ~ ", paste(colnames(df5), collapse = "+")))
# creation de l'arbre à partir, formule, et données
type_eta_propre = ctree(fmla, data = df_propre)
# print(type_eta)
# plot de l'arbre de décision
# plot(type_eta_propre, type = "simple")
# prédiction à partir de l'arbre de prédiction
table(predict(type_eta_propre), df_propre$Type.Etablissement)
##
## CH1 CH2 CH3 CH4 CHU CLC HL pr PSP
## CH1 113 1 0 0 0 0 8 5 0
## CH2 4 56 0 0 0 0 0 1 1
## CH3 0 0 32 0 0 0 0 0 0
## CH4 0 0 1 155 0 0 0 5 0
## CHU 0 0 0 0 27 0 0 0 0
## CLC 0 0 0 0 0 19 0 0 0
## HL 2 0 0 0 0 0 127 3 0
## pr 4 1 1 0 0 0 4 672 20
## PSP 3 0 0 0 0 0 0 0 4
le taux de succès que l’on obtient à partir d’un arbre que l’on a construit sur des données privées des individus dont la prédiction a été un à partir du premier arbre. s’améliore, on a un gain d’au moins 10% de succès de prédiction et on approche les 100% de succès.
(sum(predict(type_eta_propre)==df_propre$Type.Etablissement)) / nrow(df_propre)
## [1] 0.9495666
Le taux de prédiction est de $ 95% $ pour des données “nétoyées” contre $ 82% $, soit un apport de $ 13% $ de succès. Considérons ensuite ces données comme base.
df5 = df_propre[,-1]
Dans la suite on considère les données sans les individus qui n’ont pas pu être prédit par l’arbre de décisions. On les suppose abérante.
Construction des intervalles pour chaque variable
On change de reférentiel, afin de pouvoir observer un nuage de point par réduction de dimension, mieux observer les distances, et tenter une amérlioration de l’arbre de décision.
Chaque variable est divisée en 9 intervalles, qui vont contituer des modalités pour rendre les données qualitatives.
(data version 2)
# Nombre d'intervalles nint = 9
nint=9
# Methode de calcul des intervales
methodeinterv = "hclust"
# Matrice qui contiendra les bornes des intervals
interv=matrix(0,nrow = ncol(df5),ncol=nint+1)
# On calcul les intervalles, et on stock les bornes
# Pour chaque ligne on a les bornes d'intervalles une variable
for (i in 1:ncol(df5)){
interv[i,] = classIntervals(df5[,i],style = methodeinterv,n=nint)$brks
}
Transformation du tableau de données initial en tableau disjontif complet pour l’ACM.
On affecte les individus aux classes de varibles. Et on crée des noms de colonnes plus intuitives pour chaque intervalle de variable.
# Creation des noms de la colonne de la matrice disjonctif
# Les nom sont de la forme [borne inf nom_variable borne supp]
nomvarint = matrix(0, nrow = ncol(df5), ncol =ncol(interv) - 1)
for(i in 1:ncol(df5)){
for(j in 1:ncol(interv)-1){
nomvarint[i,j] = paste(interv[i,j],colnames(df5)[i],interv[i,j+1], sep = "")
}
}
nomvarint = as.vector(t(nomvarint))
# Construction du tableau disjonctif complet
# < 5 ">
# tab_disj_comp = matrix(0,nrow = nrow(df5),ncol = nint)
tab_disj_comp = array(data = "Non", dim = c(nrow(df5),nint,ncol(df5)), dimnames = NULL)
for (k in 1:ncol(df5))
{
for (l in 1:nrow(df5))
{
for (f in 1:nint)
{
if(df5[l,k]>=interv[k,f] && df5[l,k]<interv[k,f+1])
{
tab_disj_comp[l,f,k]="Oui"
}
}
}
}
tab1 = matrix(tab_disj_comp[1:nrow(df5),1:nint,1],ncol = nint,nrow = nrow(df5))
for (z in 2:dim(tab_disj_comp)[3]){
tab1 = cbind(tab1,matrix(tab_disj_comp[1:nrow(df5),1:nint,z],ncol = nint,nrow = nrow(df5)))
}
# tab1 est le tableau disjoctif complet
# On change les noms de colonnes du tableau disjonctif complet
tab1 = `colnames<-`(tab1,nomvarint)
tab1 = as.data.frame(tab1)
#head(tab1)
ACM
On effectue une ACM sur les données qualitatifs obtenues à partir des données quantitatives.
Variance apportée par axe
# ACM avec Factomine R
library(FactoMineR)
library(factoextra)
## Welcome! Related Books: `Practical Guide To Cluster Analysis in R` at https://goo.gl/13EFCZ
# ACM
res.mca = MCA(tab1, graph = FALSE, ncp = 5)
# plot variance bring per axe
fviz_screeplot(res.mca)
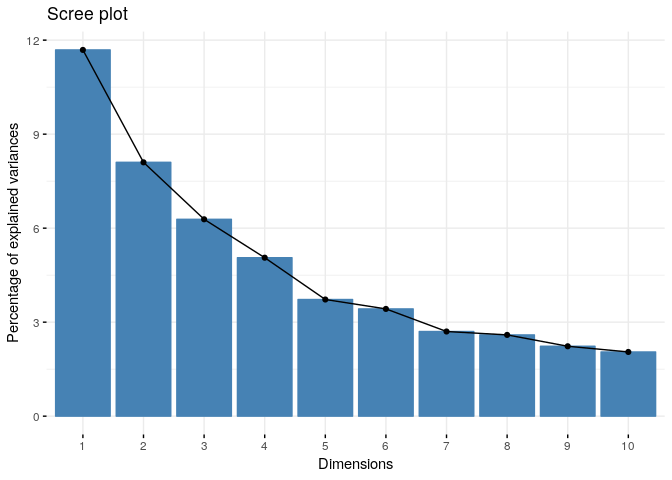
Individus et variables
# plot variable + indi
fviz_mca_biplot(res.mca)
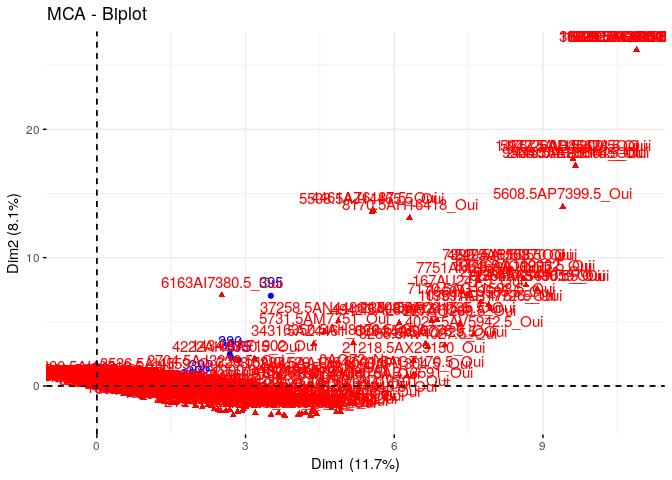
Graphique des individus
# plot indiv only
fviz_mca_ind(res.mca)
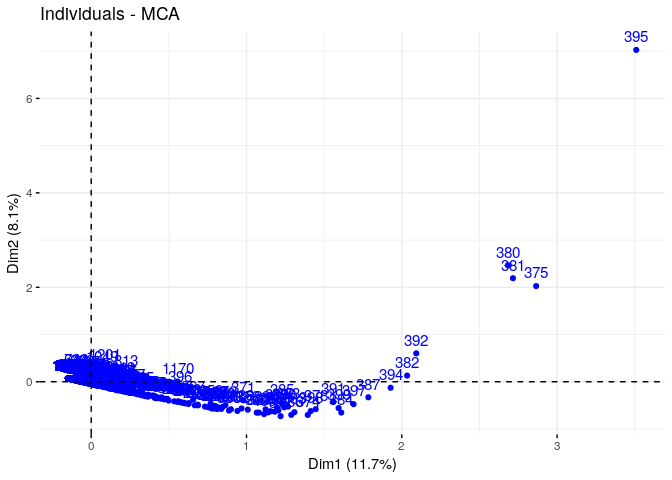
Graphique des Variables
# plot variable only
fviz_mca_var(res.mca)
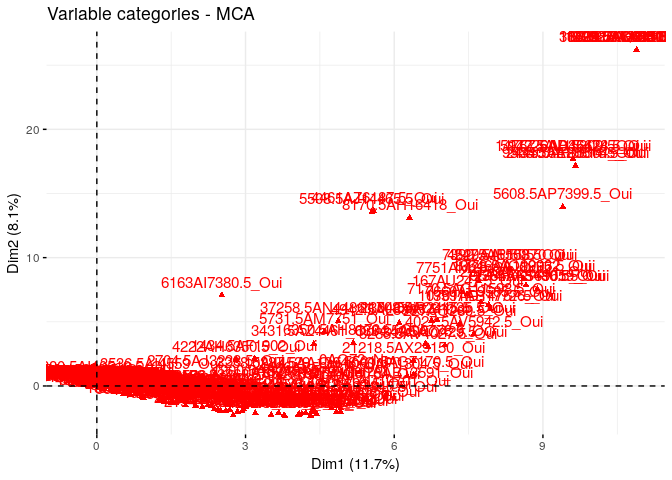
Arbres de décision et Prédiction des données issues de l’ACM sur les données initiales
Arbre de décision
A partir de l’ACM on obtients les coordonnées des individus en dimension réduite. On tente un arbre de décision sur ces coordonnées.
# Prédiction sur les données de acm
acm_ind_coord = data.frame(res.mca$ind$coord)
# On change les noms des colonnes pour pouvoir creer une formule pour la prédiction
acm_ind_coord = `colnames<-`(acm_ind_coord, c('a', 'b', 'c', 'd', 'e'))
# On colle les types d'établissement au tableau des coordonnées des ind à l'issue du mca pour generer l'arbre de décision
acm_ind_coord['Type.Etablissement'] = df_propre$Type.Etablissement
# On cré la formule qui va prédire le type d'établissement en fonction des coordonnées fournies par le mca
fmla <- as.formula(paste("Type.Etablissement ~ ", paste(c('a', 'b', 'c', 'd', 'e'), collapse = "+")))
# creation de l'arbre à partir, formule, et données
type_eta_mca = ctree(fmla, data = acm_ind_coord)
# print(type_eta_mca)
# plot de l'arbre de décision
# plot(type_eta_mca)
#plot(type_eta_mca, type = "simple")
Prédiction à partir de l’arbre (ACM)
Prédiction à partir de l’arbre. Pour une comparaison avec les l’arbre des données quantitatives.
# prédiction à partir de l'arbre de prédiction
# df5$Type.Etablissement = df5typeeta
table(predict(type_eta_mca), df_propre$Type.Etablissement)
##
## CH1 CH2 CH3 CH4 CHU CLC HL pr PSP
## CH1 113 20 0 0 0 0 0 0 0
## CH2 9 23 2 0 0 0 0 8 0
## CH3 0 2 19 5 0 0 0 1 1
## CH4 0 0 2 148 1 1 0 4 0
## CHU 0 0 0 2 26 0 0 0 0
## CLC 0 0 0 0 0 0 0 0 0
## HL 0 0 0 0 0 0 139 135 13
## pr 4 13 11 0 0 18 0 538 11
## PSP 0 0 0 0 0 0 0 0 0
Taux de réussite de la prédiction
Taux de réussite de la prédiction à partir de l’arbre obtenue sur les ACM.
(sum(predict(type_eta_mca)==df_propre$Type.Etablissement)) / nrow(df_propre)
## [1] 0.7927502
Prédiction sur le tableau de valeurs qualitatifs…
On construit un arbre de décision sur les données qualitatives (Sans ACM). On en profite pour tester le package rpart, les autres arbres ont été construit avec le package party. Rpart avec rpart.plot permet de désinner arbre plus beau.
library(rpart.plot)
tab1["Type.Etablissement"] = df_propre["Type.Etablissement"]
fmla <- as.formula(paste("Type.Etablissement ~ ", paste(sprintf("`%s`", colnames(tab1[,1:length(tab1)-1])), collapse = "+")))
# prédit type.e... en fontion de toutes les autres variables...
type_eta_mca = rpart(fmla,data=tab1,control=rpart.control(minsplit=0,cp=-100))
prp(type_eta_mca)
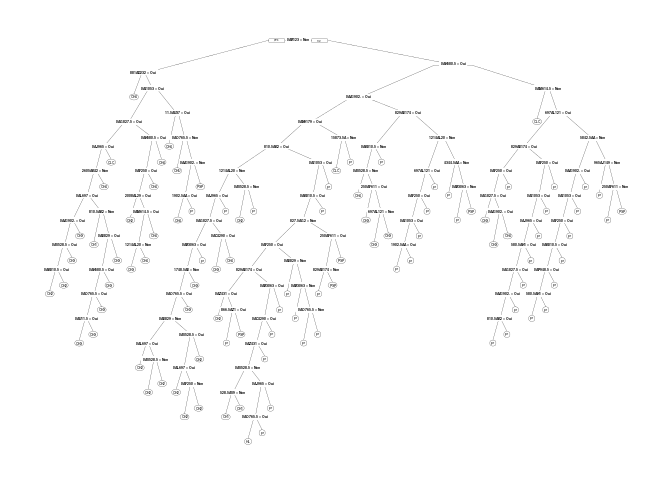
On évalue ici les performances de l’arbre en fonction du nombre de feuille, plus de feuille peut être signe de sur-apprentissage donc de baisse de performance de prédiction, vice-versa.
# Performances
plotcp(type_eta_mca)
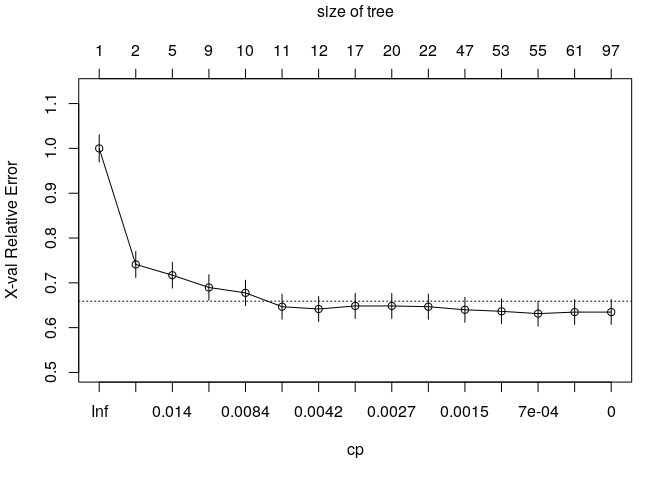
Tableau de confusion et taux de succès de prédiction, on a pas de meilleur performance que l’arbre de décision sur les données initiales, ou privé des indivdus “aberrants.”
table(tab1$Type.Etablissement, predict(type_eta_mca, tab1[,1:length(tab1)-1], type="class"))
##
## CH1 CH2 CH3 CH4 CHU CLC HL pr PSP
## CH1 3 9 0 0 0 0 113 1 0
## CH2 1 35 1 0 0 0 20 1 0
## CH3 0 5 26 0 0 0 0 3 0
## CH4 0 0 0 155 0 0 0 0 0
## CHU 0 0 0 0 27 0 0 0 0
## CLC 0 0 0 0 0 19 0 0 0
## HL 0 0 0 0 0 0 139 0 0
## pr 1 3 1 0 0 0 135 546 0
## PSP 0 0 0 0 0 0 13 3 9
(sum(predict(type_eta_mca, tab1[,1:length(tab1)-1], type="class")==df_propre$Type.Etablissement)) / nrow(df_propre)
## [1] 0.7557132
Données renéttoyées : ACM, arbre de décision, CAH, kmeans
On renettoie encore une fois les données. on supprime les variables qualitatives inutiles, c’est à dire les variables qui n’ont que très très peu d’individus ou pas, ou les variables qui ont un trop grand nombre d’individus (ce n’est pas une variable distinctive dans un contexte ou l’on cherche la distinction des individus)
On a nettoyé les données sur excel de façon manuelle. Mais le processus peut très bien être fait sur R ou python.
On repète le processus exécuté sur la version de données précédente.
(data version 3)
ACM sur les données version 3
# On nettoie les variables qualitatives... On vire les variables trop commune à tous les indivs
# on vire les variables avec 1 seul indiv et on vire l'indiv
# on vire les variables avec 0 indivs
data_new = read.csv("tab_contingences_extr.csv", sep = ";")
# head(data_new)
res.mca2 = MCA(data_new[,2:length(data_new)], graph = FALSE, ncp = 5)
# plot variance bring per axe
fviz_screeplot(res.mca2)
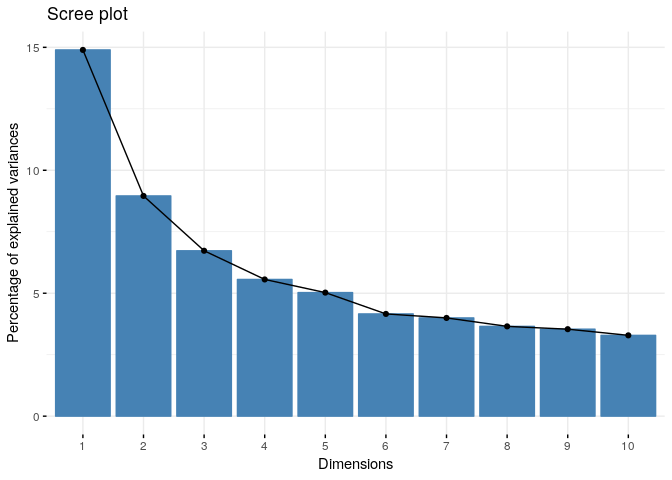
fviz_mca_biplot(res.mca2)
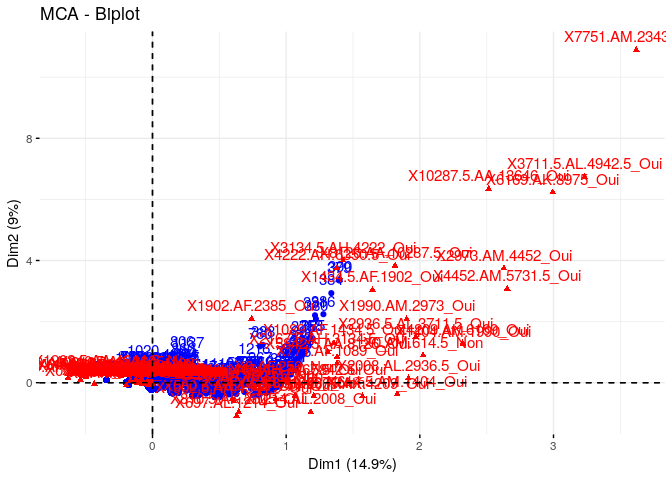
# plot indiv only
fviz_mca_ind(res.mca2, label = "none")
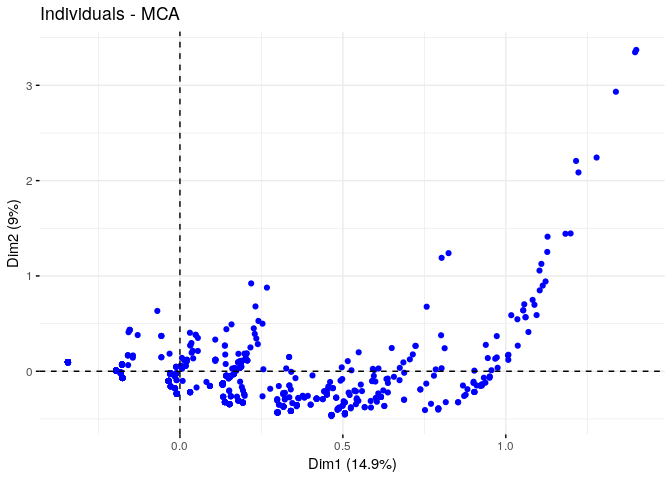
# plot variable only
fviz_mca_var(res.mca2, label = "none")

# res.hcpc = HCPC(res.mca2)
CAH
dd <- dist(res.mca2$ind$coord, method = "euclidean")
hc <- hclust(dd, method = "ward.D2")
hcd <- as.dendrogram(hc)
# Define nodePar
nodePar <- list(lab.cex = 0.6, pch = c(NA, 19),
cex = 0.7, col = "blue")
# Customized plot; remove labels
plot(hcd, ylab = "Height", nodePar = nodePar, leaflab = "none")
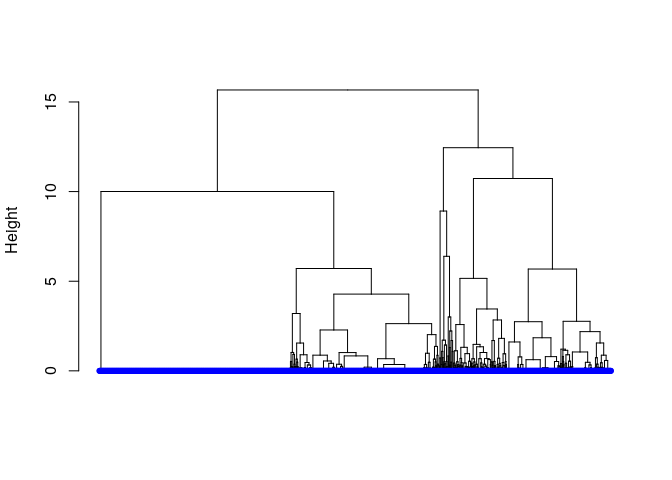
# dentrogrape circulaire
# library(ape)
#
# plot(as.phylo(hc), type = "fan")
Arbre de décision (data version 3)
Arbre, prédiction et performance de la prédiction
#data_new["Type.Etablissement"] = df_propre["Type.Etablissement"]
fmla <- as.formula(paste("Type.Etablissement ~ ", paste(sprintf("`%s`", colnames(data_new[,2:length(data_new)])), collapse = "+")))
# prédit type.e... en fontion de toutes les autres variables...
type_eta_mca = rpart(fmla,data=data_new,control=rpart.control(minsplit=2,cp=0))
# type_eta_mca = rpart(fmla,data=data_new)
prp(type_eta_mca)
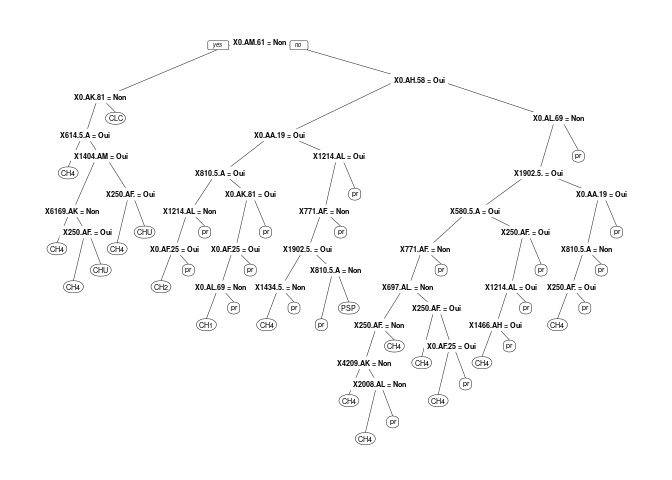
table(data_new$Type.Etablissement, predict(type_eta_mca, data_new[,2:length(data_new)], type="class"))
##
## CH1 CH2 CH3 CH4 CHU CLC HL pr PSP
## CH1 1 8 0 0 0 0 0 117 0
## CH2 0 27 0 0 0 0 0 31 0
## CH3 0 16 0 5 0 0 0 13 0
## CH4 0 2 0 140 1 0 0 12 0
## CHU 0 0 0 0 22 0 0 0 0
## CLC 0 0 0 0 0 15 0 2 0
## HL 0 0 0 0 0 0 0 139 0
## pr 0 4 0 27 0 0 0 652 0
## PSP 0 0 0 0 0 1 0 23 1
(sum(predict(type_eta_mca, data_new[,2:length(data_new)], type="class")==data_new$Type.Etablissement)) / nrow(data_new)
## [1] 0.6814932
Predic acm
prédiction sur les données de l’acm
# Prédiction sur les données de acm
acm_ind_coord = data.frame(res.mca2$ind$coord)
# On change les noms des colonnes pour pouvoir creer une formule pour la prédiction
acm_ind_coord = `colnames<-`(acm_ind_coord, c('a', 'b', 'c', 'd', 'e'))
# On colle les types d'établissement au tableau des coordonnées des ind à l'issue du mca pour generer l'arbre de décision
acm_ind_coord['Type.Etablissement'] = data_new$Type.Etablissement
# On cré la formule qui va prédire le type d'établissement en fonction des coordonnées fournies par le mca
fmla <- as.formula(paste("Type.Etablissement ~ ", paste(c('a', 'b', 'c', 'd', 'e'), collapse = "+")))
# creation de l'arbre à partir, formule, et données
type_eta_mca = rpart(fmla, data = acm_ind_coord, control=rpart.control(minsplit=2,cp=0))
prp(type_eta_mca)
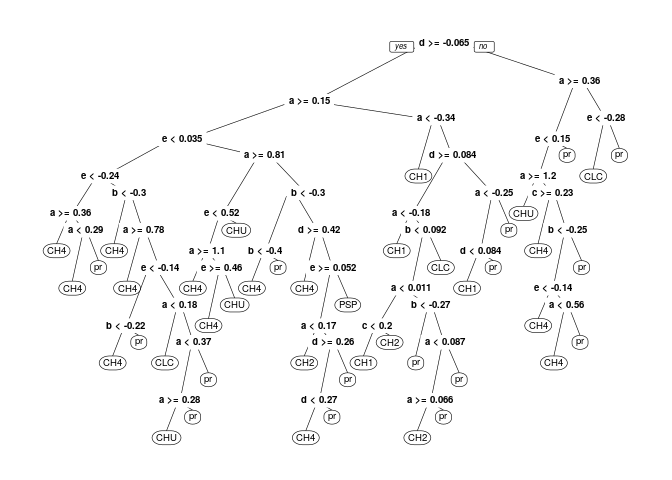
#table(predict(type_eta_mca), data_new$Type.Etablissement)
(sum(predict(type_eta_mca)==data_new$Type.Etablissement)) / nrow(data_new)
## [1] 0
kmeans, arbre de classification, et clustering.
On effectue un clustering des données d’ACM qui sont les coordonnées des individus dans le plan, et on fait des clusters.
Interprétation graphique : Ici on effectue une comparaison de nuage de point. On veut savoir si les cluster se superpose au type d’établissement. Chaque cluster correspond t-il à un type d’établissement, vice-versa? les cluster sont t-il homogènès?
# K-Means Clustering with 5 clusters
mydata = acm_ind_coord
clusters <- hclust(dist(mydata[,1:2]))
clusterCut <- cutree(clusters,9)
table(clusterCut, mydata$Type.Etablissement)
##
## clusterCut CH1 CH2 CH3 CH4 CHU CLC HL pr PSP
## 1 126 57 19 3 0 7 139 495 22
## 2 0 1 15 96 1 6 0 163 3
## 3 0 0 0 39 0 0 0 0 0
## 4 0 0 0 10 2 0 0 7 0
## 5 0 0 0 4 9 0 0 1 0
## 6 0 0 0 3 4 0 0 1 0
## 7 0 0 0 0 3 0 0 0 0
## 8 0 0 0 0 3 0 0 0 0
## 9 0 0 0 0 0 4 0 16 0
ggplot(mydata, aes(a, b, color = mydata$Type.Etablissement)) +
geom_point(alpha = 0.4, size = 3.5) + geom_point(col = clusterCut)
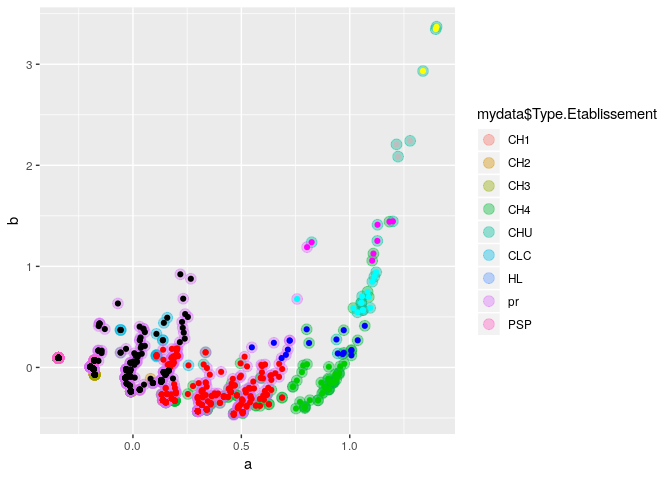
fit <- kmeans(mydata[,1:2], 9)
Ici on va visualiser les cluster obtenues
# Cluster Plot against 1st 2 principal components
# vary parameters for most readable graph
#library(cluster)
#clusplot(mydata, fit$cluster, color=TRUE, shade=TRUE,
# labels=4, lines=0)
# Centroid Plot against 1st 2 discriminant functions
library(fpc)
fpc::plotcluster(mydata[,1:2], fit$cluster)
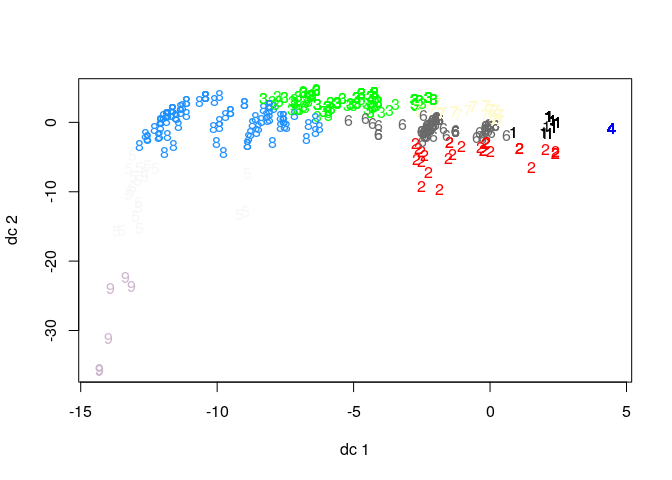
#table(predict(type_eta_mca), df_propre$Type.Etablissement)